Measurement Based Quantum Computation

In the circuit model, quantum information is processed by applying gates, which realize a coherent unitary evolution. In contrast, in Measurement Based Quantum Computation (MBQC), information is processed by sequences of adaptive single-qubit measurements performed on highly entangled multipartite states, referred to as graph states. The two models are equivalent, however the latter has no classical analogue and is uniquely quantum.

The main advantage of MBQC is found in its favorable architectural requirements for some platforms. Opposed to the application of hundreds of gates, this model shifts the complication in the state preparation step, which can be performed offline. Afterwards, the computations needs single-qubit measure, generally regarded as an easy task, and classical feed-forward electronics and modulators to implement adaptivity.

The working principle of this scheme can be understood as a generalization of the quantum teleportation, a fundamental of quantum information processing introduced in 1993¹ and demonstrated in 1999².

Quantum Teleportation

The aim of quantum teleportation is to send a quantum state from A (Alice) to B (Bob), that can be far apart and are only allowed to transmit classical information. In more detail, the quantum circuits that accomplishes the teleportation of a state
is the following:

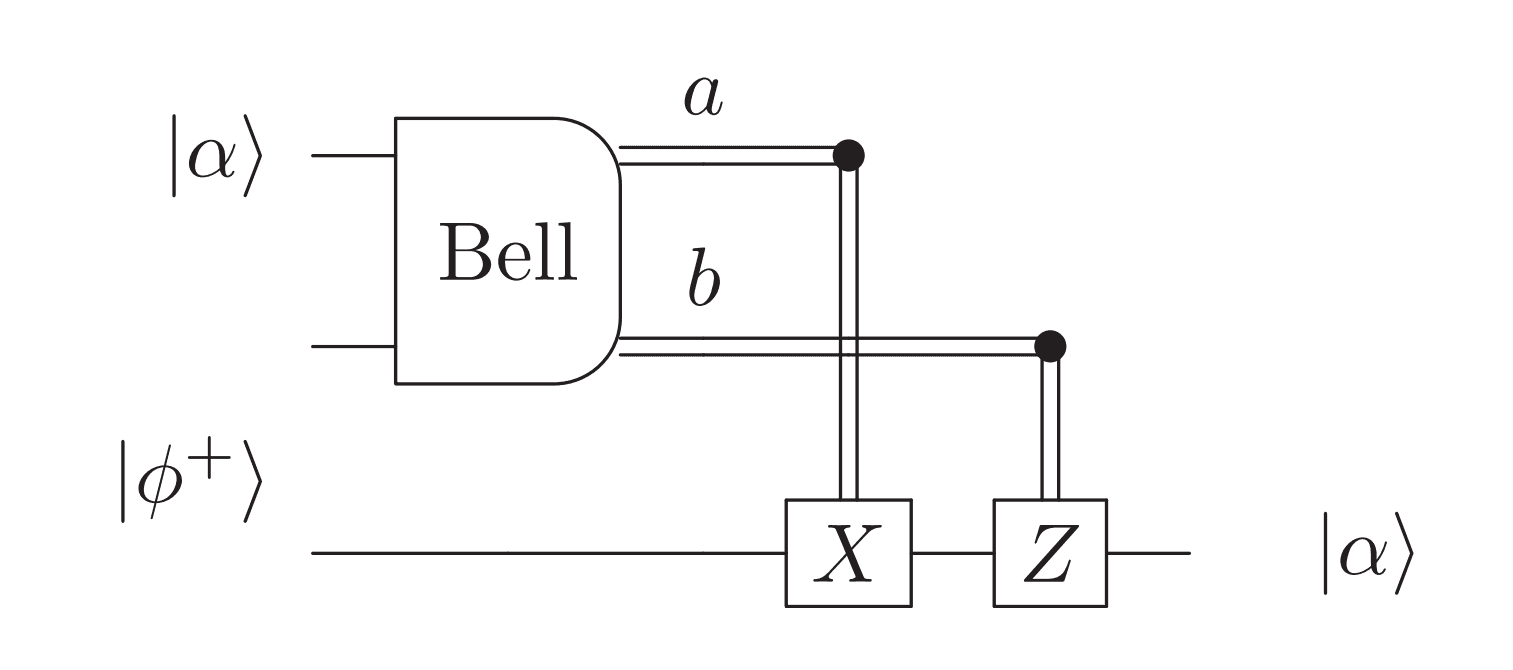
Alice performs a Bell measurement to the states she holds, then she communicates Bob the outcome of the measurement. He transforms the state he initially stored into by applying single-qubit rotations, conditioned on the measurement outcome.

Therefore, instead of directly applying a gate to a state, one can think of teleporting that state using a modified shared resource. In more detail, an operation can either be applied to a state , or that state can be teleported using the modified Bell state . The difference with the standard approach is clear: instead of performing operations on unknown states, it is just necessary to construct known states as offline resources.

Footnotes

1. Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A and Wootters W K, 1993, Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels, Phys. Rev. Lett. 70 1895–9 ↩

2. Bouwmeester D, Pan J-W, Mattle K, Eibl M, Weinfurter H and Zeilinger A, 1997, Experimental quantum teleportation, Nature, 390 575–9 ↩