Quantum Computing and Quantum Information
The Quantum Bit
In today's computers, the basic unit of information is a bit, which can be either 0 or 1. Similarily, in Quantum computing the basic unit of information is a quantum bit or qubit.
In contrast to a classical bit, a qubit can assume states of the form
where
In contrast to a classical bit, which only has either the value
The state of a qubit is considered to be a two-dimensional vector with complex entries. The so-called state vector is:
This can be specified as a linear combination of the two-dimensional standard basis vectors:
The notation
Graphical Representation of a Qubit
To represent a qubit graphically, one would naively need four dimensions, since
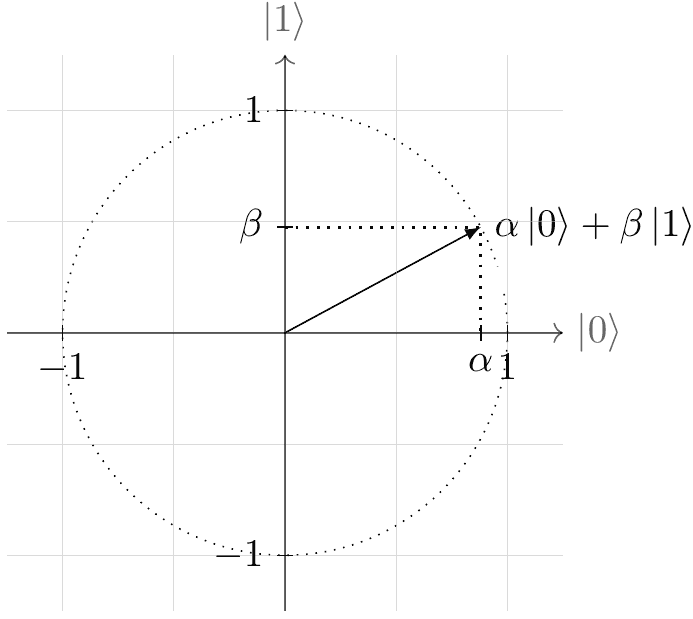
We use the value of
For a qubit with complex amplitudes, i.e.

Through transformations, we can convert the qubit formula from the previous section into the following form
where
Footnotes
Footnotes
-
Aaronson, Scott. "Introduction to quantum information science II lecture notes." (2022). Figure 3.1 ↩
-
You can look at the following to illustrate this:https://www.st-andrews.ac.uk/physics/quvis/simulations_html5/sims/blochsphere/blochsphere.html. ↩