Quantum computing with linear optics
Light has been used for centuries for various applications and it is the expertize thus gained that makes the photonic platform a mature candidate for a scalable quantum computer. Photonic chips are nowadays increasingly commonplace and photons, the particles of light, have many remarkable properties that are beneficial for their use in quantum applications. In the following, the photonic quantum computing is introduced. The central object there is a photon and the quantum computation is performed as a series of manipulations of photons by various optical elements.
Photons as carriers of quantum information
The particles of light, photons, have many different properties: they propagate in a given medium along a specific path, they carry a certain polarization, frequency, etc., and they also arrive at a given position in specific times after its creation. All these properties and more can be utilized as a representation of information. From the physical point of view, photons are almost perfect carries of information because they almost do not interact with its environment and are thus not affected by external noise and disruptions. For the same reason though, it is hard to design an efficient devices that would allows to interact photons in a controlled manner to boost the computing power of the photonic computers.
The property of choice is very often the polarization of photons - a photon can be horizontally polarized, vertically polarized, or anything in between. The polarization can also be right- or left-circular. In any case, the (pure) polarization of a given photon can be described as a quantum superposition of two extreme states that are usually denoted by
where the two complex numbers
Quantum hardware
The quantum computing on photons is performed on the lowest level by a series of optical elements such as beam splitters. These elements form building blocks for more complicated optical gates with some nice properties. These gates are in turn assembled into a specific network that corresponds to a particular quantum algorithm. In the following, all these levels of abstraction are described in detail - optical elements, optical gates, and finally computing architectures that implement quantum algorithms.
Optical elements
There are various methods how one can manipulate a beam of light - mirrors reflect the beam, lenses focus or defocus the beam, filters let through only certain colors etc. An important optical element is the beam splitter, whose photo can be seen below, which partially reflects and partially transmits the incoming beam. The exact same optical elements such as these can also be used to manipulate single photons. One has to be however more careful when describing the action of these elements - a photon is an indivisible elementary particles and cannot be divided into smaller constituents. For that reason, we cannot say that a beam splitter divides the incoming photon, transmit its part, and reflects the other. Instead, the beam splitter introduces a quantum superposition of two possibilities - either the photon is transmitted, or reflected, in such a way that these two possibilities exhibit interference: the photon behaves in a certain sense as if it was both transmitted and reflected simultaneously.

(source: Wikipedia)
Besides beam splitters and elements already mentioned, there is another class of elements that affect the photon's polarization. The most important being a polarizing beam splitter, shortened as PBS and depicted schematically below. Despite its name, its action on photons is quite different from the beam splitter: PBS transmits horizontally polarized photons and reflects the vertically polarized ones. This way we can turn the information stored in the polarization of photons into its propagation path. The last element that is crucial for quantum computing with photons is a phase delay or phase shifter - photons propagating along different paths carry with them a certain phase and a phase shifter can modify this phase. It turns out that phase shifters, mirrors and beam splitters is all one needs to implement an arbitrary unitary operation on qudits encoded into the propagation paths of a single photon.

(source: Wikipedia)
Even though there is plenty of light around us, it is not so easy to get single photons that have properties suitable for quantum computing. There are special sources of single photons, most of which is based on non-linear optical processes in special crystals. After being created, the single photons are subject to different operations by a sequence of optical elements and at the very end, the photons are detected with very sensitive single-photon detectors. This detection is not a mere readout of the photons' state. Instead, it can be seen as an integral component of the computation itself and there are many techniques that use the photon's detection as an active part of the quantum computation.
Optical gates
Optical elements mentioned in the previous section are too low-level to be usually sufficient for more advanced photon manipulation. For that reason, one usually designs a given algorithm in terms of photonic gates. These gates are small optical setups consisting of several optical elements, supplemented often by photon detectors. Notable examples of photonic gates are fusion gates that come in two types1:
Fusion type-I gate
Fusion type-I gate, also known as a parity check, takes in two photons and checks whether they reside in the same polarization - either horizontal or vertical. If they do, one photon is detected and the other is returned. The gate consists of a PBS, a wave-plate that rotates the polarization by 45 degrees, and a single-photon detector placed in one of output ports of PBS. The full setup is shown in the figure below:
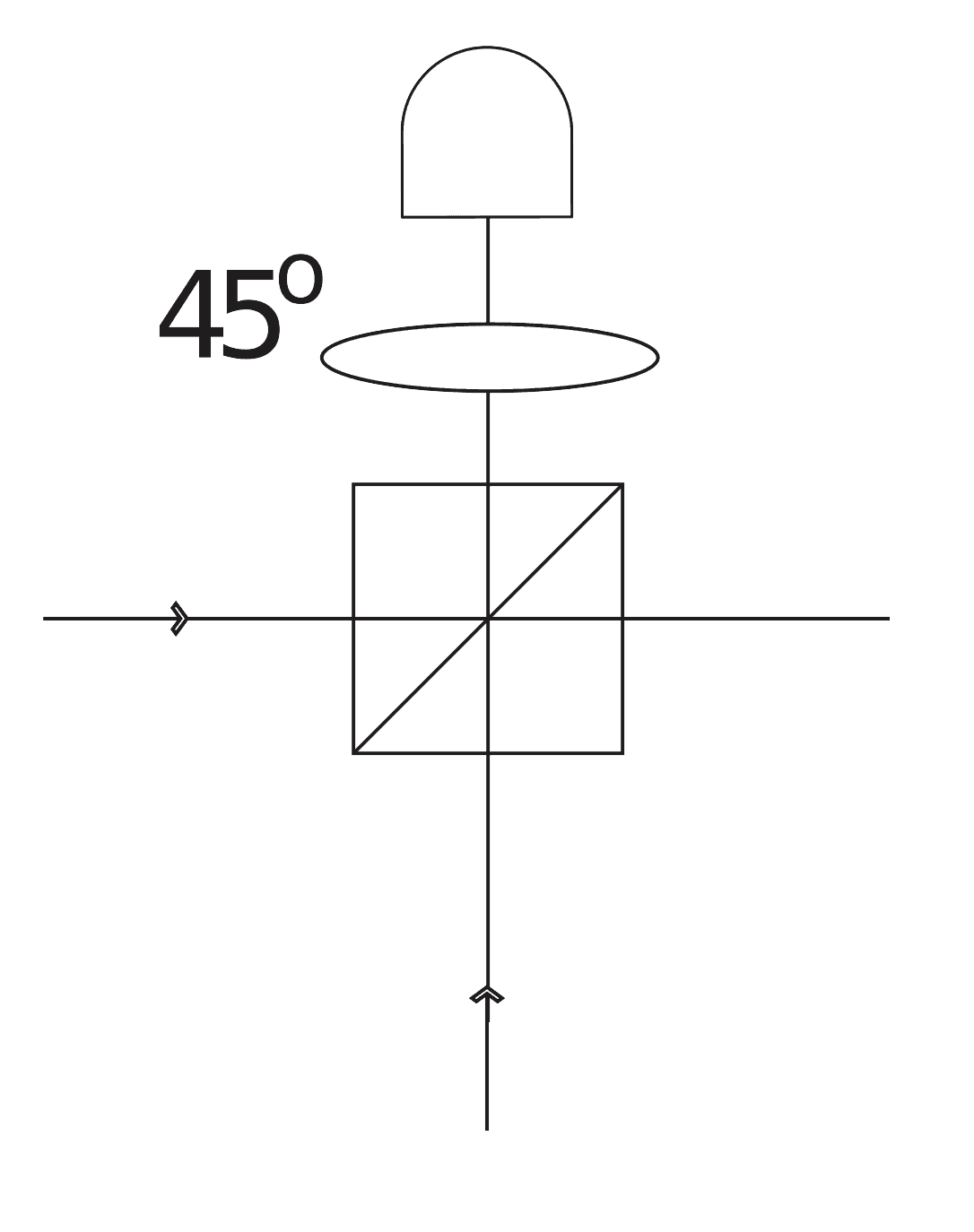
(source: ArXiv)
This gate allows to fuse two cluster states together and enables thus the generation of large cluster states, necessary for measurement-based quantum computing.
Fusion type-II gate
Fusion type-II gate is a modification of type I, where there is a wave plate at each port of PBS and both photons are detected. The setup of the gate reads explicitly:
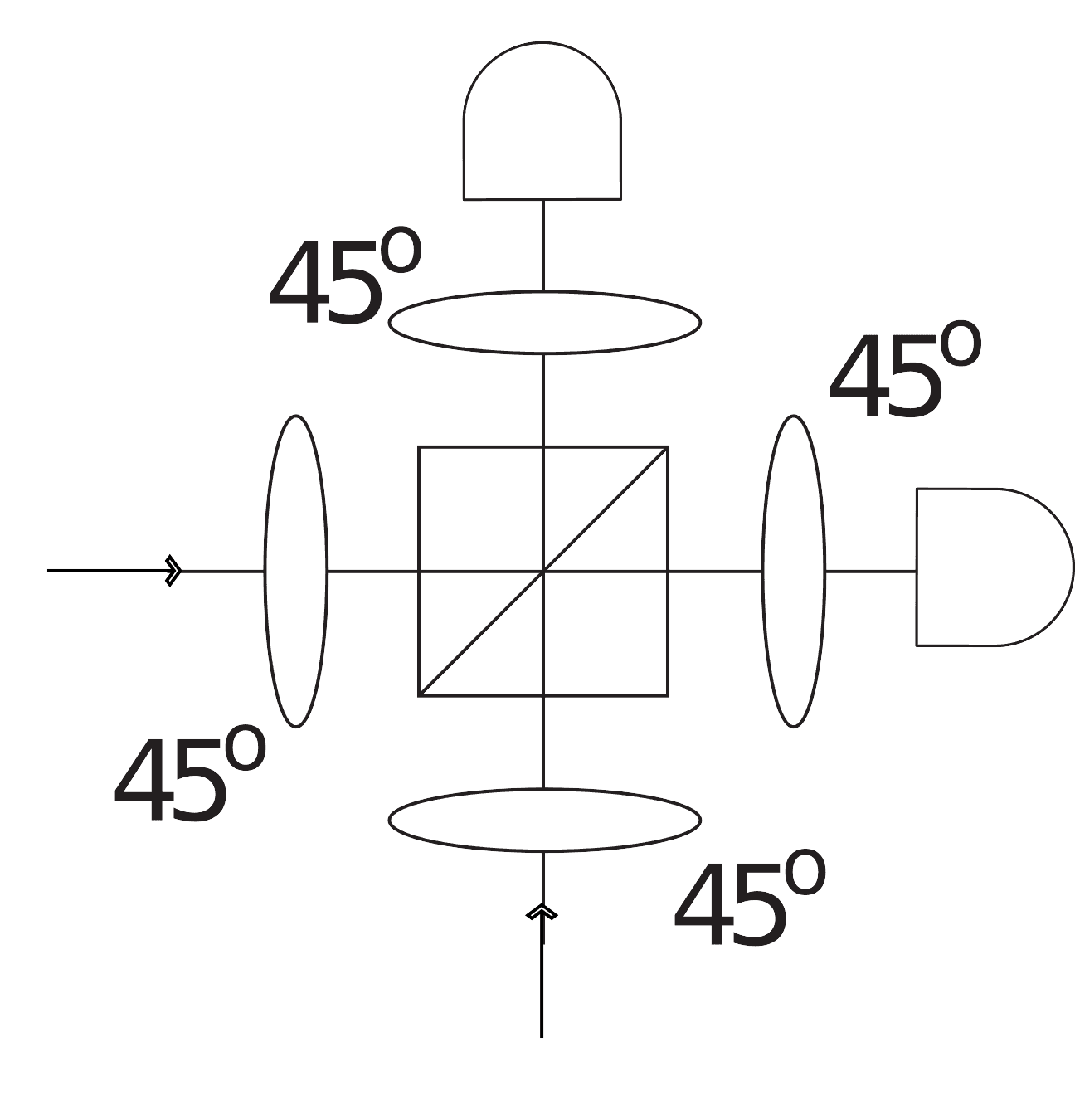
(source: ArXiv)
This gate is also used in the generation of cluster states. When exactly one photon is detected by each detector, the gate performs a projective measurement onto a maximally entangled state.
Beam splitter and HOM interference
A single beam splitter can also be seen as a gate acting on two photons. When two identical photons simultaneously impinge on a symmetric beam splitter from two different input ports, they undergo a purely quantum phenomenon called Hong-Ou-Mandel (HOM) interference. It means that the two photons never leave the beam splitter separately: either they both leave via one of both via the other output port.

Optical computing architectures
There are different computing architectures built on top of the optical elements and gates. Three of the most important architectures are presented below.
Boson sampling
Boson sampling refers to a scenario when multiple photons are injected into a huge interferometer composed of many beam splitters and subsequently detected in each of the interferometer's output ports. It can be shown that it is very hard for a classical computer to estimate the output probabilities with which the photons are detected by individual detectors2.
Boson sampling thus represents a platform for demonstrating the quantum advantage as its experimental requirements are relatively modest. On the other hand, this platform provides only restricted functionality and does not allow for the universal quantum computing.
KLM scheme
In order to achieve scalable quantum computing, it is necessary to have the ability to interact in a prescribed manner different pairs of photons. A natural candidate for such an interaction are non-linear properties of some optical media, which properties change depending on the intensity of the propagating light. Such non-linear properties are however too weak to be noticeable for single photons and as such are not suitable for real applications. What one can do instead is to incorporate a detection of a photon into the computation and use it to induce effective non-linearity. This measurement-induced non-linearity can be harnessed to perform universal quantum computation in a scheme known as KLM scheme3. The downside of this approach is that it is non-deterministic: sometimes the computation fails and has to be usually repeated many times.
Measurement-based scheme
A promising approach to quantum computing is the measurement-based scheme, where the photons are first prepared in a huge entangled state, called a cluster state, and the computation itself then consists of single-photon measurements only. The difficulty of interacting photons is thus shifted to the very beginning, that is, to the generation of the cluster state. There have been many proposal how to efficiently produce such states with photons. One of the most promising ones is the one based on fusion gates1, see above, where small cluster states are merged into larger ones by repeated applications of fusion gates.
Footnotes
-
Browne, Daniel E., and Terry Rudolph. “Resource-Efficient Linear Optical Quantum Computation.” Physical Review Letters, vol. 95, no. 1, June 2005, p. 010501. APS, https://doi.org/10.1103/PhysRevLett.95.010501. ↩ ↩2
-
Aaronson, Scott, and Alex Arkhipov. “[No Title Found].” Theory of Computing, vol. 9, no. 1, 2013, pp. 143–252. DOI.org (Crossref), https://doi.org/10.4086/toc.2013.v009a004. ↩
-
Knill, E., et al. “A Scheme for Efficient Quantum Computation with Linear Optics.” Nature, vol. 409, no. 6816, Jan. 2001, pp. 46–52. DOI.org (Crossref), https://doi.org/10.1038/35051009. ↩