Quantum Computing and Quantum Information
Quantum Gates
Similar to classical computer science, we can describe operations on qubits with gates. Some of the most important ones are the three so-called Pauli gates (also known as X-,Y- and Z-gates) and the Hadamard gate. Mathematically, the state transition is described with a unitary matrix, e.g:
This applies to simple gates on a single qubit as well as in more complex systems with several qubits.
The application of a gate
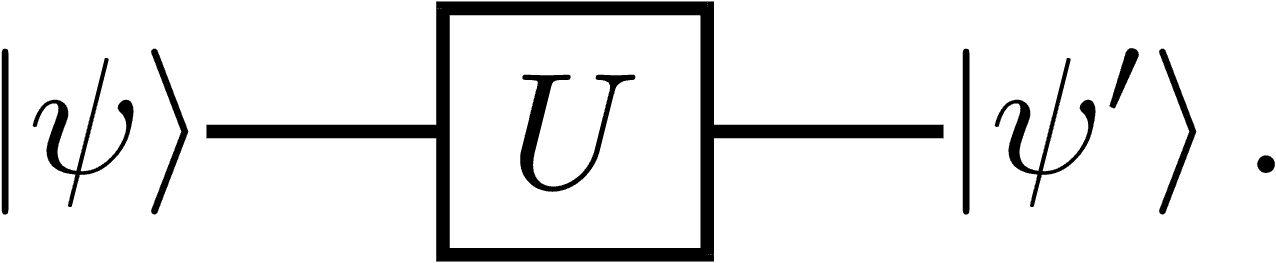
To calculate the new state
Geometrically, the application of a gate on a single qubit can be seen as a rotation of the state vector around some axis in the Bloch sphere.
Pauli Gates
X Gate
The X gate, or NOT gate, behaves similarly to a NOT gate on a
classical bit. It describes a rotation with angle
Diagram
OPENQASM 2.0; include "qelib1.inc"; qreg q[1]; x q[0];
Simulation
Not run yet
The representation as a unitary matrix is
Thus, when applied to
In Dirac notation, we write:
We can also derive this matrix by correlating the inputs and outputs in Braket notation (
We can also derive this matrix by correlating the inputs and outputs in
Braket notation (
Y Gate
In a Bloch sphere, the Y gate describes the rotation by the angle
In a circuit, it is represented as follows:
Diagram
OPENQASM 2.0; include "qelib1.inc"; qreg q[1]; y q[0];
Simulation
Not run yet
The representation as a unitary matrix is:
Applied to
In Dirac notation, we write:
Z gate
In a Bloch sphere, the Z gate describes the rotation by the angle
In a circuit, it is represented as follows:
Diagram
OPENQASM 2.0; include "qelib1.inc"; qreg q[1]; z q[0];
Simulation
Not run yet
The representation as a unitary matrix is:
Applied to
In Dirac notation, we write:
Characteristics of Pauli Gates
Together with the identity matrix, the Pauli gates form a basis of the
4-dimensional complex vector space of all complex
Hadamard Gate
The Hadamard gate, named after the French mathematician Jacques
Hadamard, plays an important role in quantum computing because it can
put a qubit from a "classical" basis state to a superposition state.
For example, an equal superposition is obtained by applying the Hadamard
gate to the state
In a circuit, it is represented as follows:
Diagram
OPENQASM 2.0; include "qelib1.inc"; qreg q[1]; h q[0];
Simulation
Not run yet
The unitary matrix is given as:
Applied to
In Dirac notation, we write:
Arbitrary Rotation Gates
A qubit can also be rotated by any angle and axis in order to "reach"
all possible states on the Bloch surface. There are different sets of
so-called universal gate sets in the literature which are sufficient for
this. We use the rotation gates
This results in the following rotation matrices:
In the circuit language, these gates look as follows:
Diagram
OPENQASM 2.0; include "qelib1.inc"; qreg q[1]; rx(pi/2) q[0]; ry(pi/2) q[0]; rz(pi/2) q[0];
Translation
Powered by Perceval, Qiskit, PyZX
Not run yet
Simulation
Not run yet
Measurement
When measuring a qubit, the respective (binary) result
Diagram
OPENQASM 2.0; include "qelib1.inc"; qreg q[1]; creg c[1]; measure q[0] -> c[0];
There is no matrix representation -- because measuring is not an operation like any other: it reads a bit of classical information from a qubit. Furthermore, in contrast to the previous gates, measurements are not reversible. In circuits, we draw a double line to distinguish classical bits from qubits.
More on measurements is described in QuBit Measurments