One-Way Quantum Computation

Among measurement-based models two slightly different approaches might be identified: the teleportation-based model, which is based on Bell-pairs and two-qubit measurements, and the one-way model which consists of single-qubit measurements on graph states. Both models are equivalent and are closely related to the teleportation primitive where, thanks to adaptive measurements performed on multipartite entangled states, arbitrary unitaries can be executed.

Instead of implementing a logic operation via unitary transformations, the same operation is executed measuring a set of ancillary qubits entangled with input qubits. The standard process of One Way Quantum Computation (OWQC) consists of three steps: prepare an entangled resource state of , measure the ancillae and correct the outputs. The third step is entirely classical and can be performed after the actual experiment, postprocessing the results.

The order and basis in which the qubits are measured dictates the implemented computation. Therefore, as measurements produce non-deterministic outcomes, every basis depends on the previous results and need to be adapted.

Example: general single-qubit transformation

In the Bloch sphere picture, any transformation single-qubit unitary can be seen as a rotation of an angle along an axis . Which, in turn, can be expressed in terms of the Euler angles¹

a sequence of rotations along the axis. The resource to perform this computation is a linear cluster state of 4 ancillary qubits entangled to the input qubit that encodes , shown in the following figure.

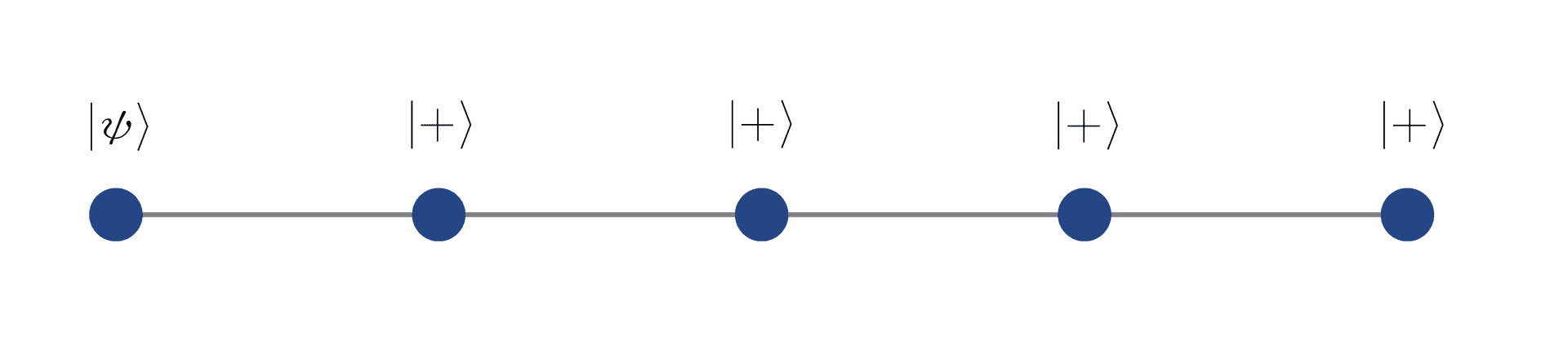
After the state generation, the computation proceeds with the measurement of the first 4 qubits in the basis described by the following operator²

Qubit	Basis	Result
1
2
3
4

defined as , i.e. . Note that the necessity to adapt the measurements is expressed, for example, by the dependence of the third basis from the result of the second measurement outcome.

After all the measurements, the state of the qubit reads , where the extra Pauli operator can eventually be erased post-processing the results of the measurement of the logic qubit.

Footnotes

1. Euler Angles Wikipedia ↩

2. Jozsa, R. ,2006, “An introduction to measurement based quantum computation.” NATO Science Series, III: Computer and Systems Sciences. Quantum Information Processing-From Theory to Experiment, 1. ↩